A Macroscopic Model of Muscle Contraction - A Letter

"Over the past two decades, while the authors – in defense of Huxley – have been rejecting the very model they now claim as their own, I have been developing the basic physical chemistry"

In my previous post (here) I described the deep conviction of scientists in their causal authority over molecules. I described a recent paper in PNAS by Debold, Walcott and colleagues (here) that perfectly illustrates their zealotry.

In this paper, their physical interpretation of their experimental results is identical to how we interpreted our experimental results 25 years ago. Their observations clearly imply that the mechanical state of muscle belongs to the system, S(t), and not to the individual molecules, s(t), in that system. They even define a system spring instead of the molecular springs that are defined in the Huxley-Hill molecular power stroke model.

Yet, as they recently wrote in a letter to the editor, they reject science “In Defense of Huxley” (here). In defense of molecular mechanics. In defense of their causal authority.

For the past 25 years, my macroscopic model, S(t), of muscle contraction has been repeatedly rejected in defense of Huxley using every logical fallacy imaginable.

So, how after “discovering” that muscle mechanics belongs to a macroscopic spring do Walcott and Debold continue to defend Huxley?

They use a rhetorical fallacy. They claim, in words alone, that muscle mechanics is molecular even though they physically define mechanics as macroscopic. This provides the false justification for rejecting my lifetime of work studying a macroscopic model of muscle contraction.

Even though I have spent the past 25 years discovering, developing and testing the very model they propose, not one of my publications is cited out of 82 references listed in their paper.

In response, I just submitted a letter to the editor to PNAS. Here is an expanded version of that letter:

A Force-Generating Switch is Not a Power Stroke

The recent article by Marang et al. (1) presents a detailed study of phosphate-induced force inhibition in muscle. While the data are useful, the interpretation suffers from a persistent and consequential mischaracterization: what the authors refer to as a “power stroke” is, in fact, not a power stroke.

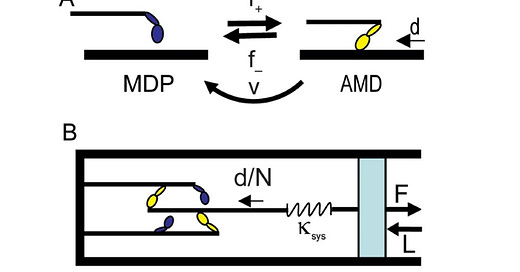
In all muscle models – including the Hill formalism (2) – power output occurs with the shortening of mechanical springs. The mechanism these authors refer to as a “power stroke” is a force-generating switch that stretches springs – the opposite of a power stroke mechanism.

A Macroscopic Power Stroke

When a force-generating switch stretches a spring assigned to that switch, the subsequent shortening of that molecular spring is Huxley’s molecular power stroke (3). When force-generating switches collectively stretch a system spring, the subsequent shortening of that system spring is a macroscopic power stroke (4).

Marang et al. describe collective force generation by an ensemble of force generating switches in a single system spring, consistent with a macroscopic power stroke model of muscle contraction. For example, to study muscle power output, FV, in their assay, they could move the optical trap at a constant velocity, V, with a constant force, F, generated by a large motor ensemble. Here, the initial shortening of the system (trap) spring with trap movement is the power stroke mechanism.

This is not Huxley’s molecular power stroke mechanism. The mechanical actions of many individual molecules are lost to one macroscopic spring. The shortening of that one macroscopic spring is – unequivocally – a macroscopic power stroke mechanism.

While a molecular power stroke occurs with the passive relaxation of a molecular spring, a macroscopic power stroke occurs with a force-dependent change in the chemistry of motors described by Boltzmann’s equation, S(t) (5, 6). My entire research career has been dedicated to studying this mechanism and showing that S(t) accurately accounts for most key aspects of muscle contraction (4, 7–9).

The lead authors are well-aware of my work. We were postdoctoral fellows in the same lab. Over the past two decades, Walcott and I have on many occasions face-to-face debated our opposing views — my macroscopic power stroke model (a system spring) versus his molecular power stroke models (molecular springs).

In Marang et al., there are no molecular springs that shorten. No molecular power strokes are possible. There is one macroscopic spring. This is the macroscopic power stroke model I developed 25 years ago (4, 10). And yet, not one of my publications is cited among the 82 references listed.

The History of a Macroscopic Power Stroke Model

In 1998, we observed and first reported that the molecular mechanism of muscle contraction is a force generating switch induced by actin binding and gated by phosphate release (11). With no attribution, this is precisely the molecular force-generating mechanism described in Marang et al.

In 1999, we demonstrated that an ensemble of force-generating switches generates force in a macroscopic spring (10). With no attribution, this is precisely the mechanism of collective force generation described in Marang et al.

In 2000, we showed that the shortening of this macroscopic spring with muscle shortening – a macroscopic power stroke – accounts for A.V. Hill’s muscle equation (4). With no attribution, this is precisely the power stroke mechanism in the authors’ model.

We demonstrated this through direct observations of the relationship between muscle force, phosphate, and the force-generating switches in muscle (9, 10, 12, 13). With no attribution, these are the very same relationships that led Marang et al. to arrive at the same conclusion 25 years later.

For decades, the lead authors have rejected a macroscopic power stroke model in defense of Huxley’s molecular power stroke model. Now they claim it as their own, completely ignoring my life’s work discovering, developing, and testing this model.

How do they rationalize this?

Through a rhetorical sleight-of-hand.

A Rhetorical Fallacy

The authors’ model irrefutably describes macroscopic springs that are stretched by an ensemble of force-generating switches – the model that I first presented as a graduate student in a platform presentation at the Biophysical Society meeting in 1998 titled “Muscle Contracts with the Flip of an Ensemble of Switches” (14).

Yet the authors and a broader scientific community have for decades been deeply invested in rejecting this macroscopic power stroke model in defense of molecular power stroke models – “In Defense of Huxley” (15).

How do they resolve this conflict? They rebrand a force-generating switch a molecular “power stroke” and ignore the actual macroscopic power stroke mechanism described by their model (16). This rhetorical gimmick allows them to present their model as part of a long tradition of molecular power stroke theories, when in fact it is a direct confirmation of a macroscopic power stroke theory that the field has systematically rejected for decades.

The reason that my life’s work discovering, developing, and testing this model is not referenced in Marang et al. is the same reason that this model and its implications have been repeatedly rejected over the past 25 years. When defending an ideology, scientific integrity is abandoned for logical fallacies.

Huxley’s molecular power stroke model cannot be defended by evidence or physics, so it has for decades been defended by the systematic rejection of both. Here, Marang et al. defend Huxley using a rhetorical fallacy: they simply rename a macroscopic power stroke model a molecular power stroke model.

They reject my life’s work because I refer to a force-generating switch as a force-generating switch and not as the misnomer “power stroke”.

The debate between my macroscopic power stroke model and Huxley’s molecular power stroke model is here reduced to one question: does myosin’s rotating lever arm generate force as a switch or power output as a stroke?

According to the math in Marang et al. it is irrefutably a force-generating switch. The power stroke is the shortening of the macroscopic spring within which the mechanical states of individual molecules are lost. Molecular power strokes are not possible.

A Micro-Macro Duality

Over the past two decades, while the authors – in defense of Huxley – have been rejecting the very model they now claim as their own, I have been developing the basic physical chemistry of this model (4–9, 12, 13, 17–26). Perhaps the authors – rather than focusing on defending Huxley – should be studying the physical chemistry of their model and its implications for interpreting their experimental results.

For example, the authors – in defense of Huxley – claim that molecular power strokes are still possible, even though the basic physical chemistry of their model clearly demonstrates that molecular and macroscopic power strokes cannot both be defined at the same time. The energy available for work must be defined on either a molecular scale or macroscopic scale. It cannot be defined on both scales at once.

After 25 years of promoting this model, I am pleased that these authors finally recognize – at least formally – that the power stroke mechanism of muscle contraction is macroscopic, and that Huxley’s molecular power stroke model is wrong. Needless to say, it is incumbent on these scientists to correct both the rhetorical fallacy and revisionist history in their article and acknowledge my 25 years of research dedicated to discovering, developing and testing this macroscopic model of muscle contraction.

References

1. C. P. Marang, D. J. Petersen, B. D. Scott, S. Walcott, E. P. Debold, Characterizing the concentration and load dependence of phosphate binding to rabbit fast skeletal actomyosin. Proceedings of the National Academy of Sciences 122 (2025).

2. T. L. Hill, Theoretical formalism for the sliding filament model of contraction of striated muscle. Part I. Prog. Biophys. Mol. Biol. 28, 267–340 (1974).

3. A. F. Huxley, Muscle structure and theories of contraction. Prog Biophys Biophys Chem 7, 255–318 (1957).

4. J. E. Baker, D. D. Thomas, A thermodynamic muscle model and a chemical basis for A.V. Hill’s muscle equation. J Muscle Res Cell Motil. 21, 335–344 (2000).

5. J. E. Baker, Thermodynamics and Kinetics of a Binary Mechanical System: Mechanisms of Muscle Contraction. Langmuir 38, 15905–15916 (2022).

6. J. E. Baker, Within Thermal Scales: The Kinetic and Energetic Pull of Chemical Entropy. BioRxiv (2023). https://doi.org/https://doi.org/10.1101/2023.09.20.558706.

7. J. E. Baker, Four Phases of a Force Transient Emerge From a Binary Mechanical System. J. Muscle Res. Cell Motil. (2024). https://doi.org/https://doi.org/10.1007/s10974-024-09674-8.

8. V. Murthy, J. E. Baker, Stochastic force generation in an isometric binary mechanical system. J Gen Physiol156 (2024).

9. J. E. Baker, The Problem with Inventing Molecular Mechanisms to Fit Thermodynamic Equations of Muscle. Int J Mol Sci 24 (2023).

10. J. E. Baker, L. E. W. LaConte, I. Brust-Mascher, D. D. Thomas, Mechanochemical coupling in spin-labeled, active, isometric muscle. Biophys J 77, 2657–64 (1999).

11. J. E. Baker, I. Brust-Mascher, S. Ramachandran, L. E. LaConte, D. D. Thomas, A large and distinct rotation of the myosin light chain domain occurs upon muscle contraction. Proc Natl Acad Sci U S A 95, 2944–9 (1998).

12. A. M. Hooft, E. J. Maki, K. K. Cox, J. E. Baker, An accelerated state of myosin-based actin motility. Biochemistry 46, 3513–20 (2007).

13. T. J. Stewart, V. Murthy, S. P. Dugan, J. E. Baker, Velocity of myosin-based actin sliding depends on attachment and detachment kinetics and reaches a maximum when myosin binding sites on actin saturate. Journal of Biological Chemistry 297, 101178 (2021).

14. J. E. Baker, Muscle contracts with the flip of an ensemble of switches. Biophys J 74, A22 (1998).

15. S. Walcott, S. Sun, E. Debold, W. Herzog, In defense of Huxley. Biophys J 123, 1–5 (2024).

16. S. Liu, et al., Modeling thick filament activation suggests a molecular basis for force depression. Biophys J123, 555–571 (2024).

17. J. E. Baker, D. D. Thomas, Thermodynamics and kinetics of a molecular motor ensemble. Biophys J 79, 1731–6 (2000).

18. J. E. Baker, C. Brosseau, P. B. Joel, D. M. Warshaw, The biochemical kinetics underlying actin movement generated by one and many skeletal muscle myosin molecules. Biophys J 82, 2134–47 (2002).

19. J. E. Baker, C. Brosseau, P. Fagnant, D. M. Warshaw, The Unique Properties of Tonic Smooth Muscle Emerge from Intrinsic as Well as Intermolecular Behaviors of Myosin Molecules. J Biol Chem 278, 28533–9 (2003).

20. T. J. Stewart, et al., Actin Sliding Velocities are Influenced by the Driving Forces of Actin-Myosin Binding. Cell Mol Bioeng 6, 26–37 (2013).

21. B. D. Haldeman, R. K. Brizendine, K. C. Facemyer, J. E. Baker, C. R. Cremo, The kinetics underlying the velocity of smooth muscle myosin filament sliding on actin filaments in vitro. J Biol Chem 289, 21055–70 (2014).

22. R. K. Brizendine, et al., Velocities of unloaded muscle filaments are not limited by drag forces imposed by myosin cross-bridges. Proceedings of the National Academy of Sciences 112, 11235–40 (2015).

23. R. K. Brizendine, et al., A mixed-kinetic model describes unloaded velocities of smooth, skeletal, and cardiac muscle myosin filaments in vitro. Sci Adv 3 (2017).

24. J. E. Baker, A chemical thermodynamic model of motor enzymes unifies chemical-Fx and powerstroke models. Biophys J 121, 1184–1193 (2022).

25. J. A. Ellsworth, J. E. Baker, Scaling in Biological Systems: A Molecular-Ensemble Duality. bioRxiv2025.01.31.635926 (2025). https://doi.org/10.1101/2025.01.31.635926.

26. J. E. Baker, A Macroscopic Quantum Heat Engine : Nested Resonant Structures and the Entropic Stability of Life. BioRxiv (2024). https://doi.org/https://doi.org/10.1101/2024.02.15.580422.